Linear algebra is essential to deep learning and scientific computing, and it’s always been a core part of PyTorch. PyTorch 1.9 extends PyTorch’s support for linear algebra operations with the torch.linalg module. This module, documented here, has 26 operators, including faster and easier to use versions of older PyTorch operators, every function from NumPy’s linear algebra module extended with accelerator and autograd support, and a few operators that are completely new. This makes the torch.linalg immediately familiar to NumPy users and an exciting update to PyTorch’s linear algebra support.
NumPy-like linear algebra in PyTorch
If you’re familiar with NumPy’s linear algebra module then it’ll be easy to start using torch.linalg. In most cases it’s a drop-in replacement. Let’s looking at drawing samples from a multivariate normal distribution using the Cholesky decomposition as a motivating example to demonstrate this:
import numpy as np
# Creates inputs
np.random.seed(0)
mu_np = np.random.rand(4)
L = np.random.rand(4, 4)
# Covariance matrix sigma is positive-definite
sigma_np = L @ L.T + np.eye(4)
normal_noise_np = np.random.standard_normal(mu_np.size)
def multivariate_normal_sample_np(mu, sigma, normal_noise):
return mu + np.linalg.cholesky(sigma) @ normal_noise
print("Random sample: ",
multivariate_normal_sample_np(mu_np, sigma_np, normal_noise_np))
: Random sample: [2.9502426 1.78518077 1.83168697 0.90798228]
Now let’s see the same sampler implemented in PyTorch:
import torch
def multivariate_normal_sample_torch(mu, sigma, normal_noise):
return mu + torch.linalg.cholesky(sigma) @ normal_noise
The two functions are identical, and we can validate their behavior by calling the function with the same arguments wrapped as PyTorch tensors:
# NumPy arrays are wrapped as tensors and share their memory
mu_torch = torch.from_numpy(mu_np)
sigma_torch = torch.from_numpy(sigma_np)
normal_noise_torch = torch.from_numpy(normal_noise_np)
multivariate_normal_sample_torch(mu_torch, sigma_torch, normal_noise_torch)
: tensor([2.9502, 1.7852, 1.8317, 0.9080], dtype=torch.float64)
The only difference is in how PyTorch prints tensors by default.
The Cholesky decomposition can also help us quickly compute the probability density function of the non-degenerate multivariate normal distribution. One of the expensive terms in that computation is the square root of the determinant of the covariance matrix. Using properties of the determinant and the Cholesky decomposition we can calculate the same result faster than the naive computation, however. Here’s the NumPy program that demonstrates this:
sqrt_sigma_det_np = np.sqrt(np.linalg.det(sigma_np))
sqrt_L_det_np = np.prod(np.diag(np.linalg.cholesky(sigma_np)))
print("|sigma|^0.5 = ", sqrt_sigma_det_np)
: |sigma|^0.5 = 4.237127491242027
print("|L| = ", sqrt_L_det_np)
: |L| = 4.237127491242028
And here’s the same validation in PyTorch:
sqrt_sigma_det_torch = torch.sqrt(torch.linalg.det(sigma_torch))
sqrt_L_det_torch = torch.prod(torch.diag(torch.linalg.cholesky(sigma_torch)))
print("|sigma|^0.5 = ", sqrt_sigma_det_torch)
: |sigma|^0.5 = tensor(4.2371, dtype=torch.float64)
print("|L| = ", sqrt_L_det_torch)
: |L| = tensor(4.2371, dtype=torch.float64)
We can measure the difference in run time using PyTorch’s built-in benchmark utility:
import torch.utils.benchmark as benchmark
t0 = benchmark.Timer(
stmt='torch.sqrt(torch.linalg.det(sigma))',
globals={'sigma': sigma_torch})
t1 = benchmark.Timer(
stmt='torch.prod(torch.diag(torch.linalg.cholesky(sigma)))',
globals={'sigma': sigma_torch})
print(t0.timeit(100))
: torch.sqrt(torch.linalg.det(sigma))
80.80 us
1 measurement, 100 runs , 1 thread
print(t1.timeit(100))
: torch.prod(torch.diag(torch.linalg.cholesky(sigma)))
11.56 us
1 measurement, 100 runs , 1 thread
Demonstrating that the approach using the Cholesky decomposition can be significantly faster. Behind the scenes, PyTorch’s linear algebra module uses OpenBLAS or MKL implementations of the LAPACK standard to maximize its CPU performance.
Autograd Support
PyTorch’s linear algebra module doesn’t just implement the same functions as NumPy’s linear algebra module (and a few more), it also extends them with autograd and CUDA support.
Let’s look at a very simple program that just computes an inverse and the gradient of that operation to show how autograd works:
t = torch.tensor(((1, 2), (3, 4)), dtype=torch.float32, requires_grad=True)
inv = torch.linalg.inv(t)
inv.backward(torch.ones_like(inv))
print(t.grad)
: tensor([[-0.5000, 0.5000],
[ 0.5000, -0.5000]])
We can mimic the same computation in NumPy by defining the autograd formula ourselves:
a = np.array(((1, 2), (3, 4)), dtype=np.float32)
inv_np = np.linalg.inv(a)
def inv_backward(result, grad):
return -(result.transpose(-2, -1) @ (grad @ result.transpose(-2, -1)))
grad_np = inv_backward(inv_np, np.ones_like(inv_np))
print(grad_np)
: [[-0.5 0.5]
[ 0.5 -0.5]]
Of course, as programs become more complicated it’s convenient to have builtin autograd support, and PyTorch’s linear algebra module supports both real and complex autograd.
CUDA Support
Support for autograd and accelerators, like CUDA devices, is a core part of PyTorch. The torch.linalg module was developed with NVIDIA’s PyTorch and cuSOLVER teams, who helped optimize its performance on CUDA devices with the cuSOLVER, cuBLAS, and MAGMA libraries. These improvements make PyTorch’s CUDA linear algebra operations faster than ever. For example, let’s look at the performance of PyTorch 1.9’s torch.linalg.cholesky vs. PyTorch 1.8’s (now deprecated) torch.cholesky:
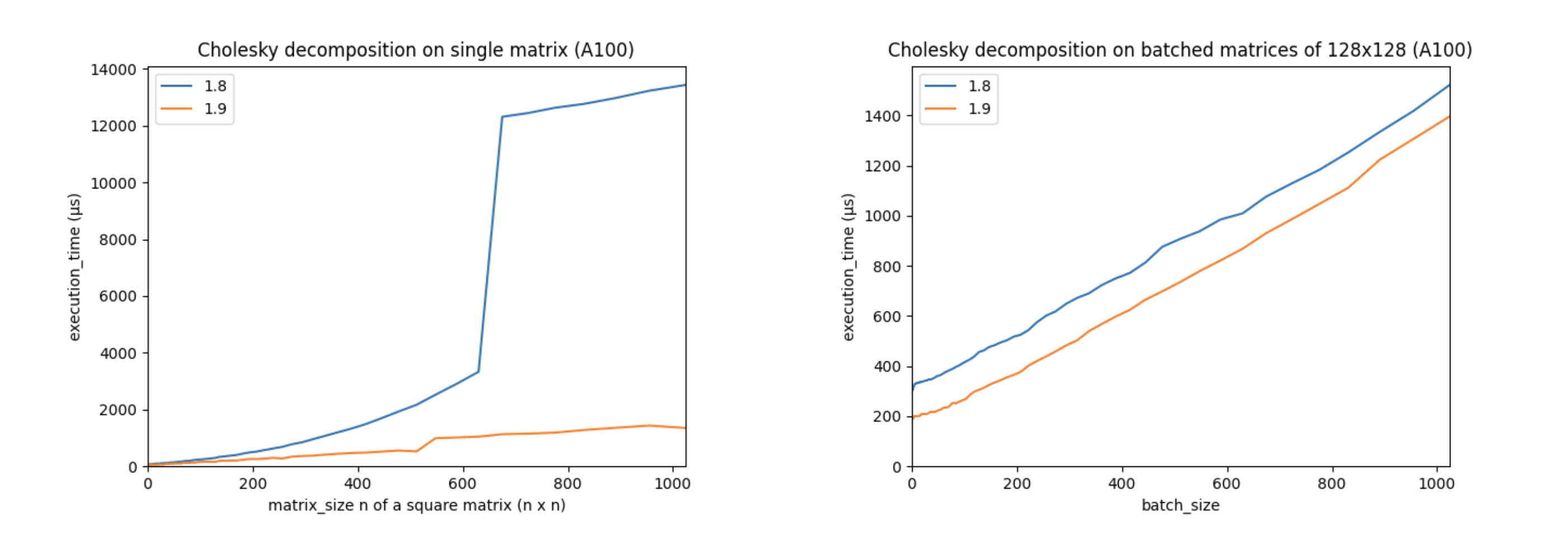
(The above charts were created using an Ampere A100 GPU with CUDA 11.3, cuSOLVER 11.1.1.58, and MAGMA 2.5.2. Matrices are in double precision.)
These charts show that performance has increased significantly on larger matrices, and that batched performance is better across the board. Other linear algebra operations, including torch.linalg.qr and torch.linalg.lstsq, have also had their CUDA performance improved.
Beyond NumPy
In addition to offering all the functions in NumPy’s linear algebra module with support for autograd and accelerators, torch.linalg has a few new functions of its own. NumPy’s linalg.norm does not allow users to compute vector norms over arbitrary subsets of dimensions, so to enable this functionality we added torch.linalg.vector_norm. We’ve also started modernizing other linear algebra functionality in PyTorch, so we created torch.linalg.householder_product to replace the older torch.orgqr, and we plan to continue adding more linear algebra functionality in the future, too.
The Future of Linear Algebra in PyTorch
The torch.linalg module is fast and familiar with great support for autograd and accelerators. It’s already being used in libraries like botorch, too. But we’re not stopping here. We plan to continue updating more of PyTorch’s existing linear algebra functionality (like torch.lobpcg) and offering more support for low rank and sparse linear algebra. We also want to hear your feedback on how we can improve, so start a conversation on the forum or file an issue on our Github and share your thoughts.
We look forward to hearing from you and seeing what the community does with PyTorch’s new linear algebra functionality!
