Welcome to the last entry into understanding the autograd engine of PyTorch series! If you haven’t read parts 1 & 2 check them now to understand how PyTorch creates the computational graph for the backward pass!
This post is based on PyTorch v1.11, so some highlighted parts may differ across versions.
PyTorch autograd graph execution
The last post showed how PyTorch constructs the graph to calculate the outputs’ derivatives w.r.t. the inputs when executing the forward pass. Now we will see how the execution of the backward pass is coordinated and done by looking at the whole process, starting from Python down to the lower C++ level internals.
What Happens when Calling backward()/grad() from Python
Using variable.backward()
After doing all our calculations with an input set to require the gradient, we call .backward() on the result to initiate the backward pass execution.
>>> x = torch.tensor([0.5, 0.75], requires_grad=True)
>>> y = torch.exp(x).sum()
>>> y.backward()
Calling .backward() on a tensor results in a call to torch.autograd.backward().
# torch/_tensor.py
def backward(self, gradient=None, retain_graph=None, create_graph=False, inputs=None):
…
torch.autograd.backward(self, gradient, retain_graph, create_graph, inputs=inputs)
torch.autograd.backward() checks the arguments and calls the autograd engine in the C++ layer.
def backward(
tensors: _TensorOrTensors,
grad_tensors: Optional[_TensorOrTensors] = None,
retain_graph: Optional[bool] = None,
create_graph: bool = False,
grad_variables: Optional[_TensorOrTensors] = None,
inputs: Optional[_TensorOrTensors] = None,
) -> None:
…
if inputs is not None and len(inputs) == 0:
raise RuntimeError("'inputs' argument to backward() cannot be empty.")
tensors = (tensors,) if isinstance(tensors, torch.Tensor) else tuple(tensors)
inputs = (inputs,) if isinstance(inputs, torch.Tensor) else \
tuple(inputs) if inputs is not None else tuple()
grad_tensors_ = _tensor_or_tensors_to_tuple(grad_tensors, len(tensors))
grad_tensors_ = _make_grads(tensors, grad_tensors_)
if retain_graph is None:
retain_graph = create_graph
Variable._execution_engine.run_backward(
tensors, grad_tensors_, retain_graph, create_graph, inputs,
allow_unreachable=True, accumulate_grad=True) # allow_unreachable flag
First, whether the grad_tensors argument was specified or not, there is a call to the _make_grads function. This is used to check the provided grad_tensors or to specify the default value for them by looking at the tensors argument values’ shapes. Check the first blog post for details on the default value for the grad_tensors of the backward pass. This function just provides the vector of the vector jacobian product if it was not initially specified.
In the above code, Variable has an _execution_engine attribute that is defined in torch.autograd.variable to be of type ImperativeEngine; the C++ engine exported to python and declared in torch/csrc/autograd/python_engine.cpp. In the following sections, we explain in detail how this object executes the backward pass.
Note that the torch.autograd.backward function has an inputs optional argument. This argument is used when we want to calculate the .grad field of only a subset of input tensors in the forward pass.
>>> x = torch.tensor([0.5, 0.75], requires_grad=True)
>>> y = torch.tensor([0.1, 0.90], requires_grad=True)
>>> z = torch.exp(x * y).sum()
>>> torch.autograd.backward([z], inputs=[x])
>>> x.grad
tensor([0.1051, 1.7676])
>>> y.grad # None
>>>
Using torch.autograd.grad
An alternative to backward() is to use torch.autograd.grad(). The main difference to backward() is that grad() returns a tuple of tensors with the gradients of the outputs w.r.t. the inputs kwargs instead of storing them in the .grad field of the tensors. As you can see, the grad() code shown below is very similar to backward.
def grad(
outputs: _TensorOrTensors,
inputs: _TensorOrTensors,
grad_outputs: Optional[_TensorOrTensors] = None,
retain_graph: Optional[bool] = None,
create_graph: bool = False,
only_inputs: bool = True,
allow_unused: bool = False,
is_grads_batched: bool = False
) -> Tuple[torch.Tensor, ...]:
outputs = (outputs,) if isinstance(outputs, torch.Tensor) else tuple(outputs)
inputs = (inputs,) if isinstance(inputs, torch.Tensor) else tuple(inputs)
overridable_args = outputs + inputs
if has_torch_function(overridable_args):
return handle_torch_function(
grad,
overridable_args,
outputs,
inputs,
grad_outputs=grad_outputs,
retain_graph=retain_graph,
create_graph=create_graph,
only_inputs=only_inputs,
allow_unused=allow_unused,
)
grad_outputs_ = _tensor_or_tensors_to_tuple(grad_outputs, len(outputs))
grad_outputs_ = _make_grads(outputs, grad_outputs_)
if retain_graph is None:
retain_graph = create_graph
if is_grads_batched:
# …. It will not be covered here
else:
return Variable._execution_engine.run_backward(
outputs, grad_outputs_, retain_graph, create_graph, inputs,
allow_unused, accumulate_grad=False) # Calls into the C++ engine to run the backward pass
Figure 1 shows the computational graph with the backward() and grad() arguments highlighted in red and blue, respectively:
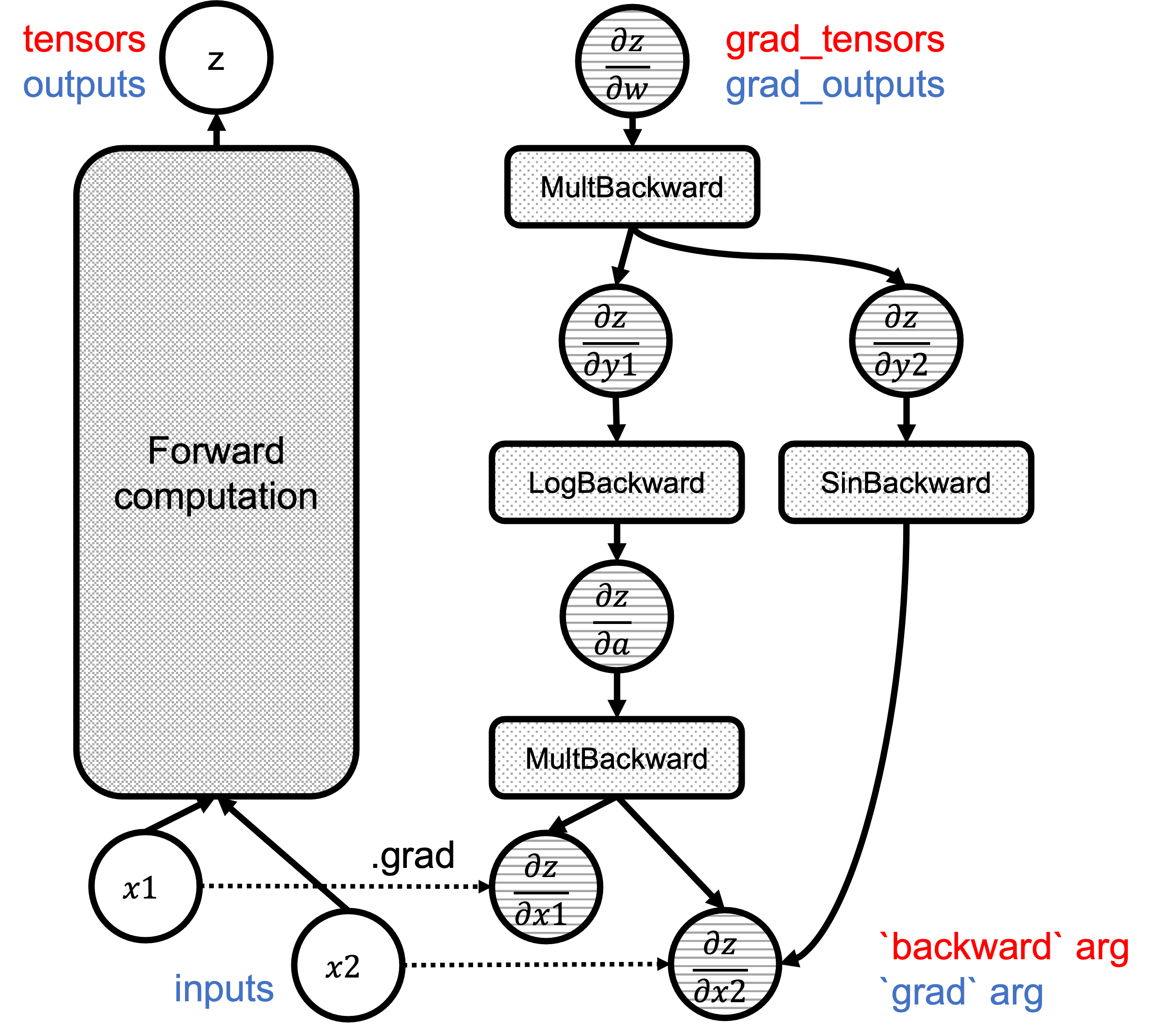
Fgiure 1: Correspondence of `backward`/`grad` arguments in the graphs.
Going Inside the Autograd Engine
Refreshing Concepts: Nodes and Edges
As we saw in 2
The computational graph comprises Node and Edge objects. Please read that post if you haven’t done it yet.
Nodes
Node objects are defined in torch/csrc/autograd/function.h, and they provide an overload of operator() for the associated function and a list of edges to do the graph traversal. Note that Node is a base class that autograd functions inherit from and override the apply method to execute the backward function.
struct TORCH_API Node : std::enable_shared_from_this<Node> {
...
/// Evaluates the function on the given inputs and returns the result of the
/// function call.
variable_list operator()(variable_list&& inputs) {
...
}
protected:
/// Performs the `Node`'s actual operation.
virtual variable_list apply(variable_list&& inputs) = 0;
…
edge_list next_edges_;
uint64_t topological_nr_ = 0;
…
There is an attribute called topological_nr_ in every node object. This number is used to optimize the graph execution as it allows to discard of graph branches under certain conditions. The topological number is the longest distance between this node and any leaf node and it is shown in Figure 2. Its main property is that for any pair of nodes x, y in a directed graph topo_nr(x) < topo_nr(y) means that there is no path from x to y. So this allows for reducing the number of paths in the graph in need of traversal. Check the topological_nr
) method comment for further details.
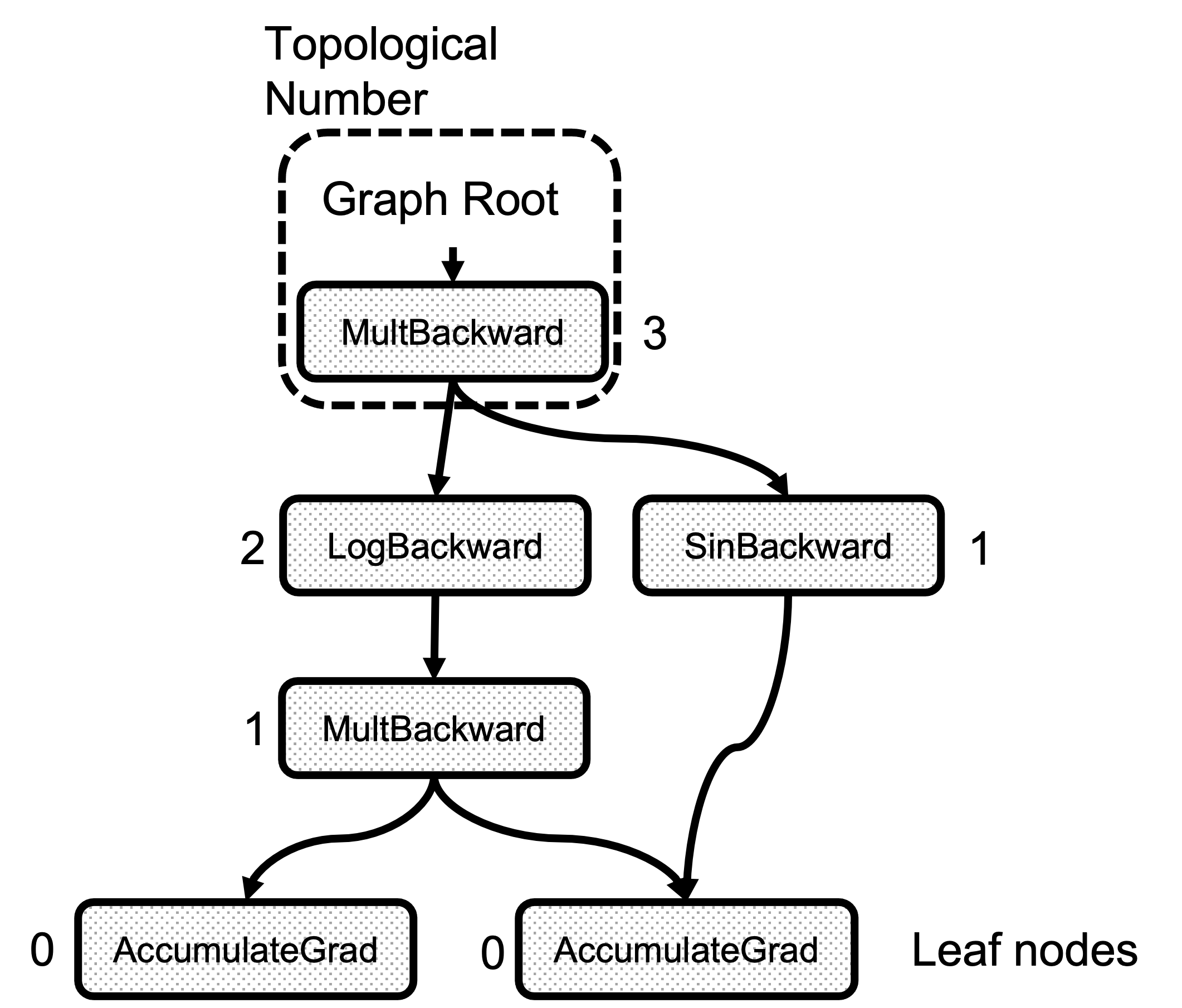
Figure 2: Example of the Topological Number calculation
Edges
The Edge object links Nodes together, and its implementation is straightforward.
struct Edge {
...
/// The function this `Edge` points to.
std::shared_ptr<Node> function;
/// The identifier of a particular input to the function.
uint32_t input_nr;
};
It only requires a function pointer to the Node and an input number that is the index of the output from the forward function this edge points to. When preparing the set of gradients before calling “function”, we know that what is flowing from this edge should be accumulated in the “input_nr”th argument. Note that the input/output name is flipped here and this is the input to the backward function.
Edge objects are constructed using the gradient_edge function method.
Edge gradient_edge(const Variable& self) {
if (const auto& gradient = self.grad_fn()) {
return Edge(gradient, self.output_nr());
} else {
return Edge(grad_accumulator(self), 0);
}
}
Entering the C++ Realm
Once that torch.autograd.backward() has been invoked, the
THPEngine_run_backward routine starts the graph traversal. Following is a schema of the function body:
PyObject *THPEngine_run_backward(PyObject *self, PyObject *args, PyObject *kwargs)
{
HANDLE_TH_ERRORS
PyObject *tensors = nullptr;
PyObject *grad_tensors = nullptr;
unsigned char keep_graph = 0;
unsigned char create_graph = 0;
PyObject *inputs = nullptr;
// Convert the python arguments to C++ objects
const char *accepted_kwargs[] = { // NOLINT
"tensors", "grad_tensors", "keep_graph", "create_graph", "inputs",
"allow_unreachable", "accumulate_grad", nullptr
};
if (!PyArg_ParseTupleAndKeywords(args, kwargs, "OObb|Obb", (char**)accepted_kwargs,
&tensors, &grad_tensors, &keep_graph, &create_graph, &inputs, &allow_unreachable, &accumulate_grad))
// Prepare arguments
for(const auto i : c10::irange(num_tensors)) {
// Check that the tensors require gradients
}
std::vector<Edge> output_edges;
if (inputs != nullptr) {
// Prepare outputs
}
{
// Calls the actual autograd engine
pybind11::gil_scoped_release no_gil;
outputs = engine.execute(roots, grads, keep_graph, create_graph, accumulate_grad, output_edges);
}
// Clean up and finish
}
First, we prepare the input arguments after converting the PyObject arguments to actual C++ objects. The tensors list contains the tensors from which we start the backward pass. These tensors are converted to edges using torch::autograd::impl::gradient_edge and added to a list called roots where the graph traversal starts.
edge_list roots;
roots.reserve(num_tensors);
variable_list grads;
grads.reserve(num_tensors);
for(const auto i : c10::irange(num_tensors)) {
PyObject *_tensor = PyTuple_GET_ITEM(tensors, i);
const auto& variable = THPVariable_Unpack(_tensor);
auto gradient_edge = torch::autograd::impl::gradient_edge(variable);
roots.push_back(std::move(gradient_edge));
PyObject *grad = PyTuple_GET_ITEM(grad_tensors, i);
if (THPVariable_Check(grad)) {
const Variable& grad_var = THPVariable_Unpack(grad);
grads.push_back(grad_var);
}
}
Now, if the inputs argument was specified in backward or we used the torch.autograd.grad api, the following code creates a list of edges to accumulate the gradients in the specified tensors at the end of the computation. The engine uses this later to optimize the execution as it doesn’t add the gradients in all the leaf nodes, just the specified ones.
std::vector<Edge> output_edges;
if (inputs != nullptr) {
int num_inputs = PyTuple_GET_SIZE(inputs);
output_edges.reserve(num_inputs);
for (const auto i : c10::irange(num_inputs)) {
PyObject *input = PyTuple_GET_ITEM(inputs, i);
const auto& tensor = THPVariable_Unpack(input);
const auto output_nr = tensor.output_nr();
auto grad_fn = tensor.grad_fn();
if (!grad_fn) {
grad_fn = torch::autograd::impl::try_get_grad_accumulator(tensor);
}
if (accumulate_grad) {
tensor.retain_grad();
}
if (!grad_fn) {
output_edges.emplace_back(std::make_shared<Identity>(), 0);
} else {
output_edges.emplace_back(grad_fn, output_nr);
}
}
}
The next step is the actual graph traversal and node function execution, and finally, the cleanup and return.
{
// Calls the actual autograd engine
pybind11::gil_scoped_release no_gil;
auto& engine = python::PythonEngine::get_python_engine();
outputs = engine.execute(roots, grads, keep_graph, create_graph, accumulate_grad, output_edges);
}
// Clean up and finish
}
Starting the Real Execution
engine.executeis present in torch/csrc/autograd/engine.cpp
There are two differentiated steps here:
Analyze the graph to find dependencies between functions Create worker threads that traverse the graph
Data Structures Used for the Execution
GraphTask
All the execution metadata is managed by the GraphTask class in torch/csrc/autograd/engine.h
struct GraphTask: std::enable_shared_from_this<GraphTask> {
std::atomic<uint64_t> outstanding_tasks_{0};
// …
std::unordered_map<Node*, InputBuffer> not_ready_;
std::unordered_map<Node*, int> dependencies_;
struct ExecInfo {
// …
};
std::unordered_map<Node*, ExecInfo> exec_info_;
std::vector<Variable> captured_vars_;
// …
std::shared_ptr<ReadyQueue> cpu_ready_queue_;
};
Here we see a series of variables dedicated to maintaining the execution state.
outstanding_tasks_ tracks the number of tasks left to be executed for the backward pass to complete. not_ready_ holds the input arguments for the Nodes that are not ready to be executed. dependencies_ track the number of predecessors that a Node has. As the count reaches 0, the Node is ready for execution; it is placed in a ready queue to be retrieved and executed later.
exec_info_ and the associated ExecInfo struct are used only when the inputs argument is specified or it is a call to autograd.grad(). They allow filter paths on the graph that are not needeed since only the gradients are calculated only for the variables in the inputs list.
captured_vars_ is where the results of the graph execution are temporarily stored if we used the torch.autograd.grad() api instead of torch.autograd.backward() since grad() returns the gradients as tensors instead of just filling the .grad field of the inputs.
NodeTask
The NodeTask struct is a basic class that holds an fn_ pointer to the node to execute, and an inputs_ buffer to store the input arguments to this function. Note that the functions executed by the backward pass are the derivatives specified in the derivatives.yaml file. or the user provided backward function when using custom functions as described in the second blog post.
The inputs_ buffer is also where the output gradients of the previously executed functions are aggregated, and it is defined as a std::vector<Variable> container with facilities to accumulate values at a given position.
struct NodeTask {
std::weak_ptr<GraphTask> base_;
std::shared_ptr<Node> fn_;
// This buffer serves as an implicit "addition" node for all of the
// gradients flowing here. Once all the dependencies are finished, we
// use the contents of this buffer to run the function.
InputBuffer inputs_;
};
GraphRoot
The GraphRoot is a special function used to hold multiple input variables in a single place. The code is pretty simple as it only acts as a container of variables.
struct TORCH_API GraphRoot : public Node {
GraphRoot(edge_list functions, variable_list inputs)
: Node(std::move(functions)),
outputs(std::move(inputs)) {
for (const auto& t : outputs) {
add_input_metadata(t);
}
}
variable_list apply(variable_list&& inputs) override {
return outputs;
}
AccumulateGrad
This function is set during the graph creation in gradient_edge when the Variable object doesn’t have a grad_fn. This is, it is a leaf node.
if (const auto& gradient = self.grad_fn()) {
// …
} else {
return Edge(grad_accumulator(self), 0);
}
The function body is defined in torch/csrc/autograd/functions/accumulate_grad.cpp and it essentially accumulates the input grads in the object’s .grad attribute.
auto AccumulateGrad::apply(variable_list&& grads) -> variable_list {
check_input_variables("AccumulateGrad", grads, 1, 0);
…
at::Tensor new_grad = callHooks(variable, std::move(grads[0]));
std::lock_guard<std::mutex> lock(mutex_);
at::Tensor& grad = variable.mutable_grad();
accumulateGrad(
variable,
grad,
new_grad,
1 + !post_hooks().empty() /* num_expected_refs */,
[&grad](at::Tensor&& grad_update) { grad = std::move(grad_update); });
return variable_list();
}
}} // namespace torch::autograd
accumulateGrad
does several checks on the tensors format and eventually performs the variable_grad += new_grad; accumulation.
Preparing the graph for execution
Now, let’s walk through Engine::execute. The first thing to do besides arguments consistency checks is to create the actual GraphTask object we described above. This object keeps all the metadata of the graph execution.
auto Engine::execute(const edge_list& roots,
const variable_list& inputs,
bool keep_graph,
bool create_graph,
bool accumulate_grad,
const edge_list& outputs) -> variable_list {
validate_outputs(roots, const_cast<variable_list&>(inputs), [](const std::string& msg) {
return msg;
});
// Checks
auto graph_task = std::make_shared<GraphTask>(
/* keep_graph */ keep_graph,
/* create_graph */ create_graph,
/* depth */ not_reentrant_backward_call ? 0 : total_depth + 1,
/* cpu_ready_queue */ local_ready_queue);
// If we receive a single root, skip creating extra root node
// …
// Prepare graph by computing dependencies
// …
// Queue the root
// …
// launch execution
// …
}
After creating the GraphTask, we use its associated function if we only have one root node. If we have multiple root nodes, we create a special GraphRoot object as described before.
bool skip_dummy_node = roots.size() == 1;
auto graph_root = skip_dummy_node ?
roots.at(0).function :
std::make_shared<GraphRoot>(roots, inputs);
The next step is to fill the dependencies_ map in the GraphTask object since the engine must know when it can execute a task. The outputs here is the inputs argument passed to the torch.autograd.backward() call in Python. But here, we have reversed the names since the gradients w.r.t. the inputs of the forward pass are now the outputs of the backward pass. And from now on, there is no concept of forward/backward, but only graph traversal and execution.
auto min_topo_nr = compute_min_topological_nr(outputs);
// Now compute the dependencies for all executable functions
compute_dependencies(graph_root.get(), *graph_task, min_topo_nr);
if (!outputs.empty()) {
graph_task->init_to_execute(*graph_root, outputs, accumulate_grad, min_topo_nr);
}
Here we preprocess the graph for the execution of the nodes. First, compute_min_topological_nr is called to to obtain the minimum topological number of the tensors specified in outputs (0 if no inputs kwarg was supplied to .backward or input for .grad). This computation prunes paths in the graph that lead to input variables of which we don’t want/need to calculate the grads.
Second, is the compute_dependencies call. This function is a very simple graph traversal that starts with the root Node, and for each of the edges in node.next_edges() it increments the counter in dependencies_. Figure 3 shows the result of the dependencies calculation for the example graph. Note that the number of dependencies of any node is just the number of edges arriving at it.
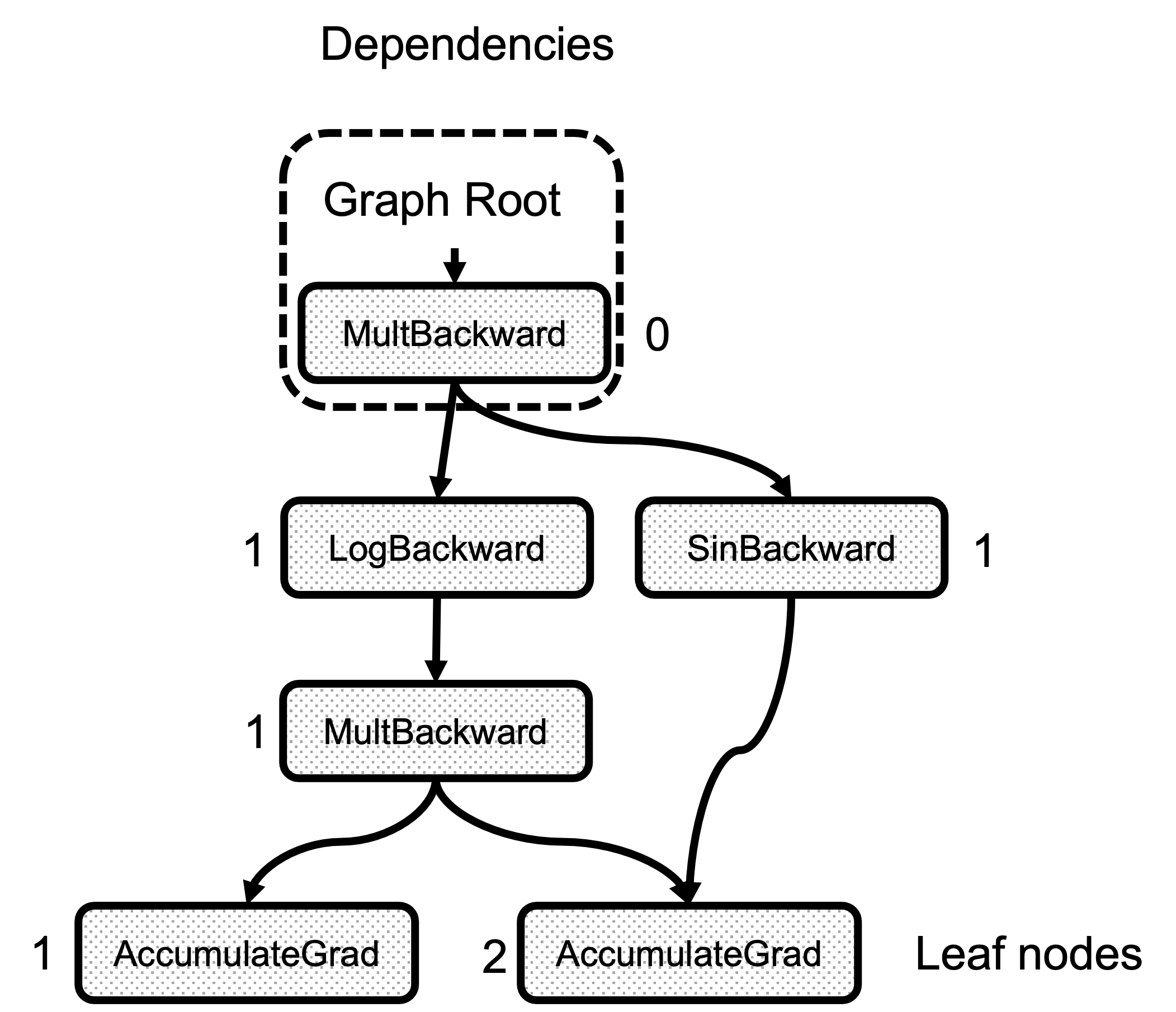
Figure 3: Number of dependencies for each node
Finally, the init_to_execute call, this is the one that populates the GraphTask::exec_info_ map in case that inputs were specified in the python backward call. It iterates the graph again, starting from the root, and records in the exec_info_ map the intermediate nodes needed to calculate only the given inputs gradients.
// Queue the root
if (skip_dummy_node) {
InputBuffer input_buffer(roots.at(0).function->num_inputs());
auto input = inputs.at(0);
input_buffer.add(roots.at(0).input_nr,
std::move(input),
input_stream,
opt_next_stream);
execute_with_graph_task(graph_task, graph_root, std::move(input_buffer));
} else {
execute_with_graph_task(graph_task, graph_root, InputBuffer(variable_list()));
}
// Avoid a refcount bump for the Future, since we check for refcount in
// DistEngine (see TORCH_INTERNAL_ASSERT(futureGrads.use_count() == 1)
// in dist_engine.cpp).
auto& fut = graph_task->future_result_;
fut->wait();
return fut->value().toTensorVector();
}
And now, we are ready to start the actual execution by creating the InputBuffer. In case we only have one root variable, we begin by copying the value of the inputs tensor (this is the gradients passed to python backward) in position 0 of the input_buffer. This is a small optimization that avoids running the RootNode for no reason. Also, if the rest of the graph is not on the cpu, we directly start on that worker while the RootNode is always placed on the cpu ready queue. Details of the workers and ready queues are explained in the section below.
On the other hand, if we have multiple roots, the GraphRoot object also holds the inputs, so it is enough to pass it an empty InputBuffer.
Graph Traversal and Node Execution
Devices, Threads and Queues
Before diving into the actual execution, we need to see how the engine is structured.
First of all, the engine is multithreaded with one thread per device. For example, the caller thread is associated with the CPU while additional threads are created and associated with each GPU or other devices available in the system. Each thread tracks its device using thread-local storage in the worker_device variable. In addition, the threads have a queue of tasks to be executed also located in thread-local storage, the local_ready_queue. This is where work is queued for this thread to execute in the thread_main function that is explained later.
You will wonder how the device where a task should be executed is decided. The InputBuffer class has a device() function that returns the first non-cpu device of all its tensors.
This function is used together with Engine::ready_queue to select the queue to queue a task.
auto Engine::ready_queue(std::shared_ptr<ReadyQueue> cpu_ready_queue, at::Device device) -> std::shared_ptr<ReadyQueue>{
if (device.type() == at::kCPU || device.type() == at::DeviceType::Meta) {
return cpu_ready_queue;
} else {
// See Note [Allocating GPUs to autograd threads]
return device_ready_queues_.at(device.index());
}
}
The ReadyQueue object is defined in torch/csrc/autograd/engine.h and it is a simple wrapper over std::priority_queue that allows a thread to wait for a task if it’s empty. One interesting property of the ReadyQueue is that it increases the GraphTask::outstanding_tasks_ value used to determine if the execution has completed or not.
auto ReadyQueue::push(NodeTask item, bool incrementOutstandingTasks) -> void {
{
std::lock_guard<std::mutex> lock(mutex_);
if (incrementOutstandingTasks) {
std::shared_ptr<GraphTask> graph_task = item.base_.lock();
++graph_task->outstanding_tasks_;
}
heap_.push(std::move(item));
}
not_empty_.notify_one();
}
auto ReadyQueue::pop() -> NodeTask {
std::unique_lock<std::mutex> lock(mutex_);
not_empty_.wait(lock, [this]{ return !heap_.empty(); });
auto task = std::move(const_cast<NodeTask&>(heap_.top())); heap_.pop();
return task;
}
Reentrant Backward
A reentrant backward happens when one of the tasks in a backward pass calls again backward. It is not a very common case, but it can be used to reduce memory utilization as it could potentially avoid saving intermediate results. For more information, check this PyTorch forum post.
class ReentrantBackward(torch.autograd.Function):
@staticmethod
def forward(ctx, input):
return input.sum()
@staticmethod
def backward(ctx, input):
# Let's compute the backward by using autograd
input = input.detach().requires_grad_()
with torch.enable_grad():
out = input.sum()
out.backward() # REENTRANT CALL!!
return out.detach()
Here, we call backward() inside backward() for a user custom-defined autograd function.
This situation can lead to deadlocks because the first backward needs to wait for the second one to complete. But some internal implementation details can prevent the second backward from completing as it is explained in the dedicated subsection.
Thread Initialization
execute_with_graph_task is in charge of initializing the threads taking care of the computation and placing the root node in the queue of the device that produced it.
c10::intrusive_ptr<at::ivalue::Future> Engine::execute_with_graph_task(
const std::shared_ptr<GraphTask>& graph_task,
std::shared_ptr<Node> graph_root,
InputBuffer&& input_buffer) {
initialize_device_threads_pool();
// Lock mutex for GraphTask.
std::unique_lock<std::mutex> lock(graph_task->mutex_);
auto queue = ready_queue(graph_task->cpu_ready_queue_, input_buffer.device());
if (worker_device == NO_DEVICE) {
set_device(CPU_DEVICE);
graph_task->owner_ = worker_device;
queue->push(NodeTask(graph_task, std::move(graph_root), std::move(input_buffer)));
lock.unlock();
thread_main(graph_task);
worker_device = NO_DEVICE;
} else {
// This deals with reentrant backwards, we will see it later.
}
return graph_task->future_result_;
}
First, this function initializes several threads (one per device) calling initialize_device_threads_pool() where several things happen:
One ReadyQueue per device is created.
One thread per non-cpu device is created.
A thread local worker_device variable is set to track the current device associated with the thread.
thread_main function is called, and threads wait for tasks to be put in their queues.
Then it retrieves the queue to place the root node based on the device that holds the tensors present in the input_buffer using the ready_queue function. Now, the main thread (the one also executing the Python interpreter) has its worker_device set to NO_DEVICE, and it is in charge of executing functions with all its tensors living in the cpu. If worker_device is set to any other value, the graph execution is already started, and .backward() was called inside a running Node, creating a reentrant backward call. This is explained later. For now,
the main thread places the task in the queue and call thread_main.
Where the Magic Happens
It’s been a long way, but finally, we are ready to traverse the graph and execute the nodes. Each of the spawned threads, and the main thread call thread_main.
auto Engine::thread_main(const std::shared_ptr<GraphTask>& graph_task) -> void {
while (graph_task == nullptr || !graph_task->future_result_->completed()) {
std::shared_ptr<GraphTask> local_graph_task;
{
NodeTask task = local_ready_queue->pop();
if (task.isShutdownTask_) {
break;
}
if (!(local_graph_task = task.base_.lock())) {
// GraphTask for function is no longer valid, skipping further
// execution.
continue;
}
if (task.fn_ && !local_graph_task->has_error_.load()) {
at::ThreadLocalStateGuard tls_guard(local_graph_task->thread_locals_);
try {
GraphTaskGuard guard(local_graph_task);
NodeGuard ndguard(task.fn_);
{
evaluate_function(
local_graph_task,
task.fn_.get(),
task.inputs_,
local_graph_task->cpu_ready_queue_);
}
} catch (std::exception& e) {
thread_on_exception(local_graph_task, task.fn_, e);
}
}
}
// Decrement the outstanding tasks.
--local_graph_task->outstanding_tasks_;
// Check if we've completed execution.
if (local_graph_task->completed()) {
local_graph_task->mark_as_completed_and_run_post_processing();
auto base_owner = local_graph_task->owner_;
if (worker_device != base_owner) {
std::atomic_thread_fence(std::memory_order_release);
ready_queue_by_index(local_graph_task->cpu_ready_queue_, base_owner)
->push(NodeTask(local_graph_task, nullptr, InputBuffer(0)));
}
}
}
}
The code here is simple, given the local_ready_queue assigned to each thread in thread-local storage. The threads loop until there are no tasks left to execute in the graph. Note that for device-associated threads, the passed graph_task argument is nullptr, and they block in local_ready_queue->pop() until a task is pushed in their queue. After some consistency checks (the task type is shutdown, or the graph is still valid). We get to the actual function invocation in evaluate_function.
try {
GraphTaskGuard guard(local_graph_task);
NodeGuard ndguard(task.fn_);
{
evaluate_function(
local_graph_task,
task.fn_.get(),
task.inputs_,
local_graph_task->cpu_ready_queue_);
}
} catch (std::exception& e) {
thread_on_exception(local_graph_task, task.fn_, e);
}
}
After calling evaluate_function, we check if the graph_task execution is complete by looking the outstanding_tasks_ number. This number increases when a task is pushed to a queue and is decreased in local_graph_task->completed() when a task is executed. When the execution is done, we return the results that are be in the captured_vars_ in case we called torch.autograd.grad() instead of torch.autograd.backward() as this function returns tensors instead of storing them in the .grad attribute of the inputs. Finally we wake up the main thread if it’s waiting by sending a dummy task.
// Decrement the outstanding tasks.
--local_graph_task->outstanding_tasks_;
// Check if we've completed execution.
if (local_graph_task->completed()) {
local_graph_task->mark_as_completed_and_run_post_processing();
auto base_owner = local_graph_task->owner_;
if (worker_device != base_owner) {
std::atomic_thread_fence(std::memory_order_release);
ready_queue_by_index(local_graph_task->cpu_ready_queue_, base_owner)
->push(NodeTask(local_graph_task, nullptr, InputBuffer(0)));
}
}
Calling the Function and Unlocking New Tasks
evaluate_function serves three purposes:
Run the function.
Accumulate its results in the next node InputBuffers.
Decrease the dependencies counter of the next nodes and enqueues the tasks reaching 0 to be executed.
void Engine::evaluate_function(
std::shared_ptr<GraphTask>& graph_task,
Node* func,
InputBuffer& inputs,
const std::shared_ptr<ReadyQueue>& cpu_ready_queue) {
// If exec_info_ is not empty, we have to instrument the execution
auto& exec_info_ = graph_task->exec_info_;
if (!exec_info_.empty()) {
// Checks if the function needs to be executed
if (!fn_info.needed_) {
// Skip execution if we don't need to execute the function.
return;
}
}
auto outputs = call_function(graph_task, func, inputs);
auto& fn = *func;
if (!graph_task->keep_graph_) {
fn.release_variables();
}
Initially, we check the exec_info_ map of the GraphTask structure to determine if the current node needs to be executed. Remember that if this map is empty, all the nodes are executed because we are calculating the grads for all the inputs of the forward pass.
After this check, the function is executed by running call_function. Its implementation is very straightforward and calls the actual derivative function and registered hooks if any.
int num_outputs = outputs.size();
if (num_outputs == 0) {
// Records leaf stream (if applicable)
return;
}
if (AnomalyMode::is_enabled()) {
// check for nan values in result
}
Next, we check the outputs of the function after call_function is done. If the number of outputs is 0, there are no following nodes to be executed so we can safely return. This is the case of the AccumulateGrad node associated with the leaf nodes.
Also, the check for NaN values in the gradients is done here if requested.
std::lock_guard<std::mutex> lock(graph_task->mutex_);
for (const auto i : c10::irange(num_outputs)) {
auto& output = outputs[i];
const auto& next = fn.next_edge(i);
if (!next.is_valid()) continue;
We have now executed a grad_fn that has returned one gradient per each of the associated forward pass function inputs. As we saw in the previous blog post, we have an Edge object per each of these input tensors, and the grad_fn of the function producing them in the forward pass. Essentially, Output[0] of the node in the backward pass, corresponds to the first argument of the forward pass associated function. Figure 4 shows how the outputs of a backward function are related to the inputs of the forward function. See that the outputs of grad_fn C are the gradients of z w.r.t. the inputs of Function C
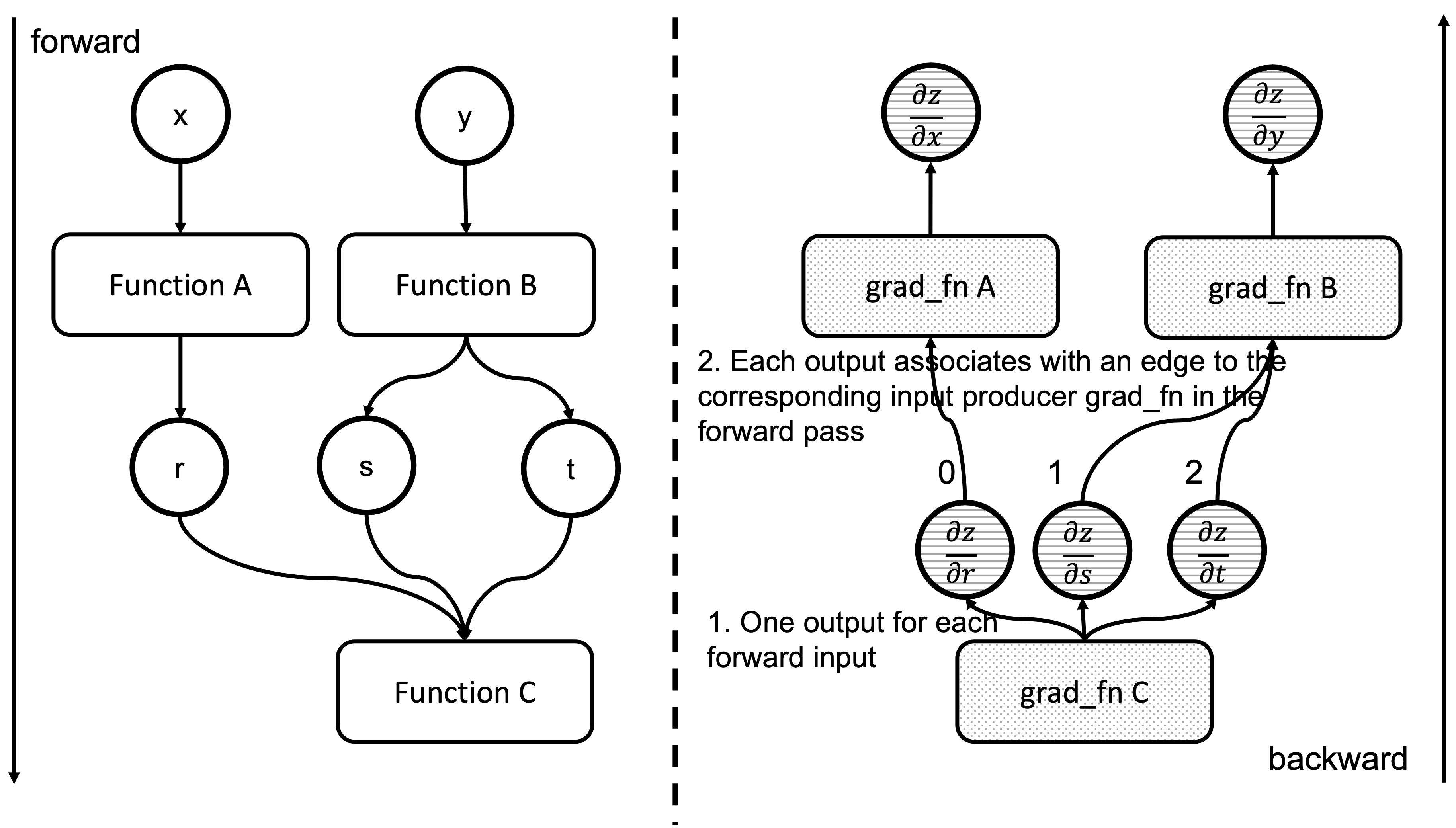
Figure 4: Correspondence between forward and backward functions inputs and outputs
We now iterate through these edges and check if the associated functions are ready to be executed.
// Check if the next function is ready to be computed
bool is_ready = false;
auto& dependencies = graph_task->dependencies_;
auto it = dependencies.find(next.function.get());
if (it == dependencies.end()) {
auto name = next.function->name();
throw std::runtime_error(std::string("dependency not found for ") + name);
} else if (--it->second == 0) {
dependencies.erase(it);
is_ready = true;
}
auto& not_ready = graph_task->not_ready_;
auto not_ready_it = not_ready.find(next.function.get());
For this, we check the graph_task->dependencies_ map. We decrement the counter, and if it reaches 0, we mark the function pointed by the edge ready to be executed. Following, we prepare the input buffers of the tasks indicated by the next edges.
if (not_ready_it == not_ready.end()) {
if (!exec_info_.empty()) {
// Skip functions that aren't supposed to be executed
}
// Creates an InputBuffer and moves the output to the corresponding input position
InputBuffer input_buffer(next.function->num_inputs());
input_buffer.add(next.input_nr,
std::move(output),
opt_parent_stream,
opt_next_stream);
if (is_ready) {
auto queue = ready_queue(cpu_ready_queue, input_buffer.device());
queue->push(
NodeTask(graph_task, next.function, std::move(input_buffer)));
} else {
not_ready.emplace(next.function.get(), std::move(input_buffer));
}
Here, we look for the task in the graph_task->not_ready_ map. If it is not present, we create a new InputBuffer object and set the current output in the input_nr position of the buffer associated with the edge. If the task is ready to be executed, we enqueue it in the appropriate device ready_queue and complete the execution. However, if the task is not ready and we have seen it before, it is present in the not_ready_map_.
} else {
// The function already has a buffer
auto &input_buffer = not_ready_it->second;
// Accumulates into buffer
input_buffer.add(next.input_nr,
std::move(output),
opt_parent_stream,
opt_next_stream);
if (is_ready) {
auto queue = ready_queue(cpu_ready_queue, input_buffer.device());
queue->push(NodeTask(graph_task, next.function, std::move(input_buffer)));
not_ready.erase(not_ready_it);
}
}
}
}
In this case, we accumulate the output in the existing input_buffer instead of creating a new one. Once all the tasks are processed, the worker thread exits the loop and complete.
All this process is summarized in the animation in Figure 5. We see how a thread peeks at the tasks in the ready queue and decrements the next nodes’ dependencies, unlocking them for execution.
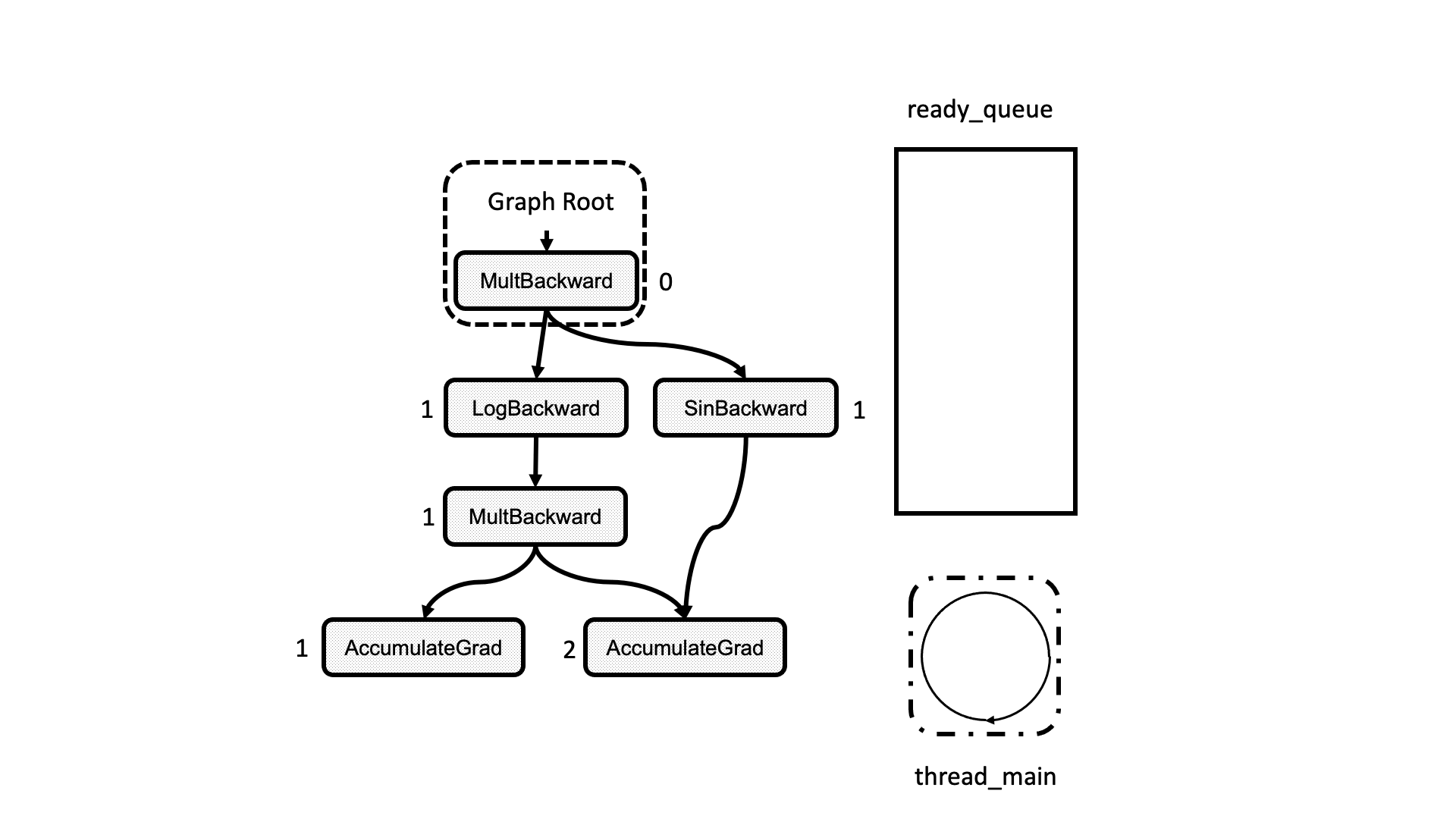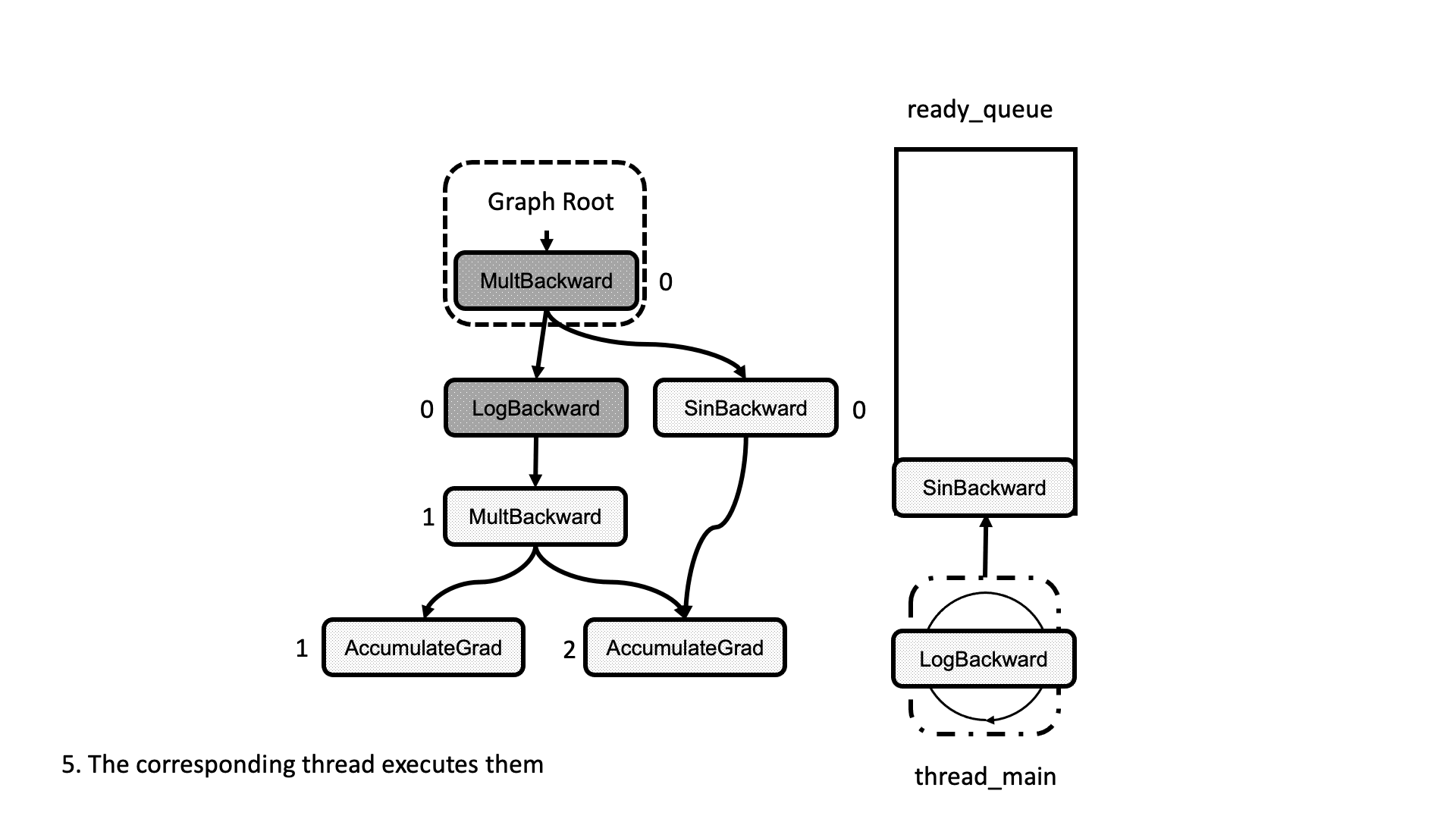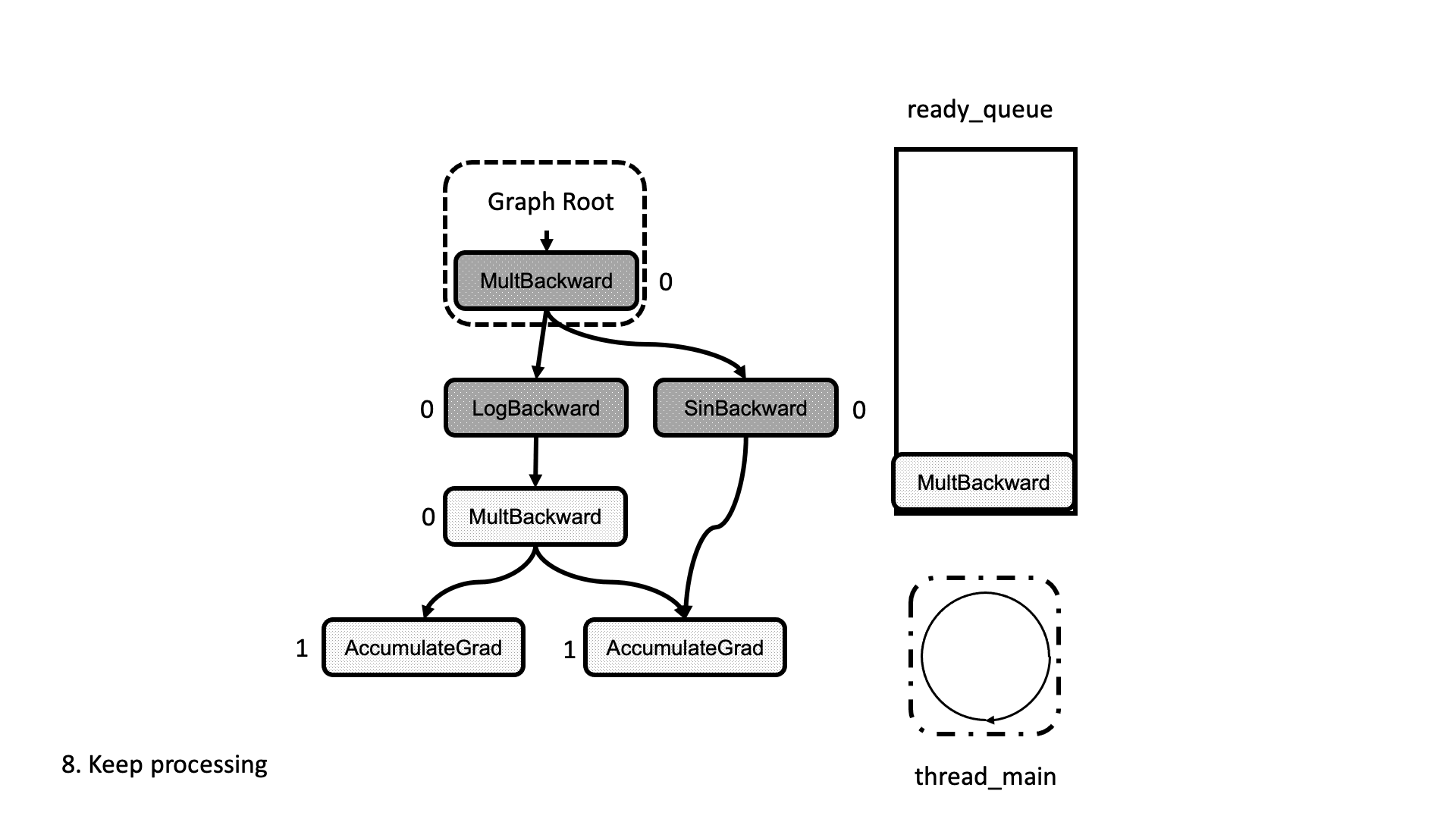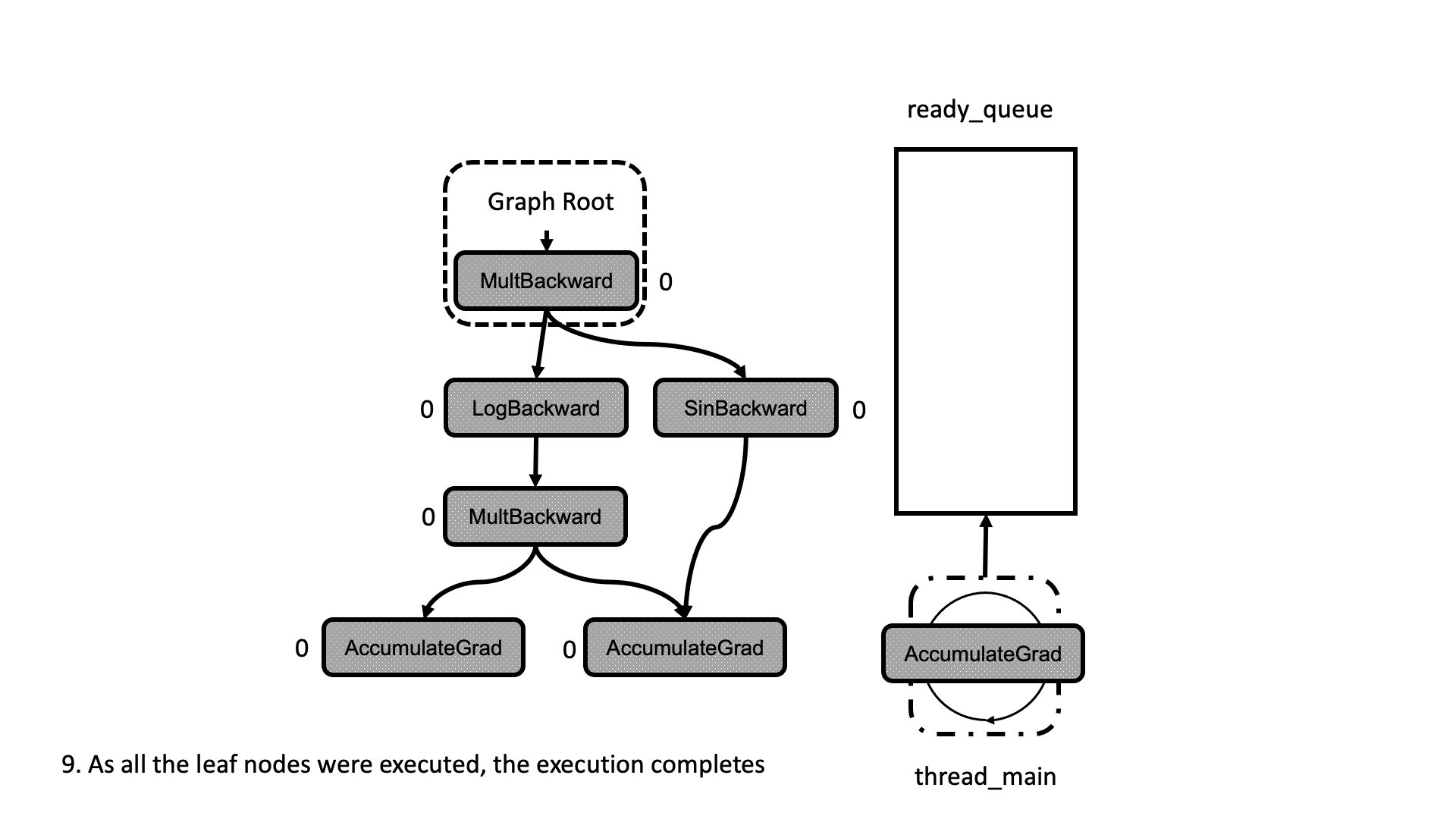
Figure 5: Animation of the execution of the computational graph
Flow with Reentrant Backward
As we saw above, the reentrant backward problem is when the currently executed function does a nested call to backward. When this happens, the thread running this function goes all the way down to execute_with_graph_task as in the non-reentrant case, but here is when things are different.
c10::intrusive_ptr<at::ivalue::Future> Engine::execute_with_graph_task(
const std::shared_ptr<GraphTask>& graph_task,
std::shared_ptr<Node> graph_root,
InputBuffer&& input_buffer) {
initialize_device_threads_pool();
// Lock mutex for GraphTask.
std::unique_lock<std::mutex> lock(graph_task->mutex_);
auto queue = ready_queue(graph_task->cpu_ready_queue_, input_buffer.device());
if (worker_device == NO_DEVICE) {
//Regular case
} else {
// If worker_device is any devices (i.e. CPU, CUDA): this is a re-entrant
// backward call from that device.
graph_task->owner_ = worker_device;
// Now that all the non-thread safe fields of the graph_task have been populated,
// we can enqueue it.
queue->push(NodeTask(graph_task, std::move(graph_root), std::move(input_buffer)));
if (current_depth >= max_recursion_depth_) {
// If reached the max depth, switch to a different thread
add_thread_pool_task(graph_task);
} else {
++total_depth;
++current_depth;
lock.unlock();
thread_main(graph_task);
--current_depth;
--total_depth;
}
}
return graph_task->future_result_;
}
Here, execute_with_graph_task detects this as a reentrant call and then looks for the current number of nested calls. If it exceeds the limit, we create a new thread to take care of the execution of this graph, and if not, we execute this reentrant call regularly.
The limit of nested calls was originally set to avoid stack overflow due to reentrant calls creating very large call stacks. However, the number was further reduced when sanitizer tests were added because of the maximum amount of locks a thread can hold at a given moment. This can be seen in torch/csrc/autograd/engine.h.
When this maximum depth is exceeded, a new thread is created with the add_thread_pool_task function.
void Engine::add_thread_pool_task(const std::weak_ptr<GraphTask>& graph_task) {
std::unique_lock<std::mutex> lck(thread_pool_shared_->mutex_);
// if we have pending graph_task objects to be processed, create a worker.
bool create_thread = (thread_pool_shared_->num_workers_ <= thread_pool_shared_->graphtasks_queue_.size());
thread_pool_shared_->graphtasks_queue_.push(graph_task);
lck.unlock();
if (create_thread) {
std::thread t(&Engine::reentrant_thread_init, this);
t.detach();
}
thread_pool_shared_->work_.notify_one();
}
Before going in-depth, let’s look at the thread_pool_shared_ object in the Engine which manages all the information related to the threads associated to the reentrant backward calls.
struct ThreadPoolShared {
unsigned int num_workers_;
std::condition_variable work_;
std::mutex mutex_;
std::queue<std::weak_ptr<GraphTask>> graphtasks_queue_;
// NOLINTNEXTLINE(cppcoreguidelines-pro-type-member-init)
ThreadPoolShared() : num_workers_(0) {}
};
ThreadPoolShared is a simple container holding a queue of GraphTask objects with synchronization mechanisms and the number of current workers.
Now it is easy to understand how add_thread_pool_task creates a thread when there are graph_task objects enqueued and insufficient workers to process them.
add_thread_pool_task initializes a thread by executing reentrant_thread_init
void Engine::reentrant_thread_init() {
at::init_num_threads();
auto tp_shared = thread_pool_shared_;
while(true) {
std::unique_lock<std::mutex> lk(tp_shared->mutex_);
++thread_pool_shared_->num_workers_;
tp_shared->work_.wait(lk, [&tp_shared]{ return !tp_shared->graphtasks_queue_.empty();});
--thread_pool_shared_->num_workers_;
auto task = tp_shared->graphtasks_queue_.front();
tp_shared->graphtasks_queue_.pop();
lk.unlock();
std::shared_ptr<GraphTask> graph_task;
if (!(graph_task = task.lock())) {
continue;
}
set_device(graph_task->owner_);
// set the local_ready_queue to the ready queue on the graph_task->owner_ device
local_ready_queue = ready_queue_by_index(graph_task->cpu_ready_queue_, graph_task->owner_);
total_depth = graph_task->reentrant_depth_;
thread_main(graph_task);
}
}
The code is straightforward. The newly created thread waits on the thread_pool_shared->graphtasks_queue_ for reentrant backward graphs to be available and executes them. Notice that this thread uses the task-ready queue associated with the device of the thread that started this call by accessing the graph_task->owner_ field set in the execute_with_graph_task function.
Error Handling
Whenever an error happens in one of the worker threads. It will be propagated to the backward calling thread.
To achieve this, there is a try/catch block in the thread_main that catches any exception in the Node function call and sets it to the associated GraphTask object.
try {
…
GraphTaskGuard guard(local_graph_task);
NodeGuard ndguard(task.fn_);
{
evaluate_function(
…
}
} catch (std::exception& e) {
thread_on_exception(local_graph_task, task.fn_, e);
}
}
}
thread_on_exception and the functions it calls end up setting the exception in the local_graph_task object.
void Engine::thread_on_exception(
std::shared_ptr<GraphTask> graph_task,
const std::shared_ptr<Node>& fn,
std::exception& e) {
graph_task->set_exception(std::current_exception(), fn);
}
void GraphTask::set_exception_without_signal(const std::shared_ptr<Node>& fn) {
if (!has_error_.exchange(true)) {
if (AnomalyMode::is_enabled() && fn) {
fn->metadata()->print_stack(fn->name());
}
}
}
void GraphTask::set_exception(
std::exception_ptr eptr,
const std::shared_ptr<Node>& fn) {
set_exception_without_signal(fn);
if (!future_completed_.exchange(true)) {
// NOLINTNEXTLINE(performance-move-const-arg)
future_result_->setError(std::move(eptr));
}
}
In set_exception it sets the has_error_ flag to true and it calls the setError
function of the future_result_ object. This will make the error to be re-thrown at the caller thread when future_result_->value() is accessed.
IValue value() {
std::unique_lock<std::mutex> lock(mutex_);
AT_ASSERT(completed());
if (eptr_) {
std::rethrow_exception(eptr_);
}
return value_;
}
Closing Remarks
This has been the last post of this series covering how PyTorch does the auto differentiation. We hope you enjoyed reading it and that now you are familiar enough with PyTorch internals to start contributing in PyTorch development!
